 |
 |
 |
 |
 |
 |
 |
 |
Introduction |
 |
 |
 |
 |
 |
 |
 |
 |
We have learned that the object medial loci that are an important aspect
of our research (see Bibliography), have advantages in intuitiveness with
their basis on figures (main figures, protrusions, indentations) and ability
to achieve locality, in capturing solidity, in their geometric power of
carrying local orientation and size information, and in robustness due
to their two-sidedness. The disadvantages of medial loci are that if they
are not to suffer the traditional weaknesses of sensitivity to boundary
detail and image noise, they cannot by themselves represent the object
at small scale and the search for a reliable, automatic means of defining
a subdivision of an object into figures continues. Also, they cannot handle
parts of objects with unpaired boundaries in the image or in the actual
geometry. In addition, since boundaries are implied rather than explicit,
boundary mechanics such as abutment and intersection are not as easily
handled as boundary representations.
While in the past we have focused on the height ridges of medialness
that we have named "cores", we now focus especially on medial methods based
on m-reps, which are trees of nets of medial atoms, with each net representing
a figure. The m-reps deformation methods that our lab now has in place
for both segmentation and shape measurement include coarse-to-fine multiscale
approaches based on Markov random fields, both geometric and statistical
object difference metrics, and intensity match metrics of both the type
reflecting just differences and those reflecting variabilities in the model.
We have also begun work on mechanical object difference metrics, aimed
at segmentations of a patient based on a model of that very patient.
 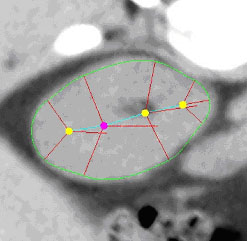 |
| Fig. 1. An m-rep model for a kidney. Left, in 3D: the m-rep
is made from 2 linked figures, each of which is represented by a mesh or
chain of medial atoms. Here the two figures represent the whole kidney
and the pelvis + ureter. The medial atoms are shown in white with the meshes
in green and the medially implied boundaries in blue. Right, in 2D: a cut
through the 3D image data showing 2D medial atoms interpolated from the
3D atoms for the figure representing the whole kidney. |
Among the m-reps programs in place are ones for building a 3D multifigure
m-reps model (see Fig. 1 for an example) for an object from a training
image with the object segmented, as well as a program for segmentation
in a target image by deformation, in a coarse-to-fine sequence, via optimization
of an objective function summing a structure typicality term and an image
match term. The steps of the coarse-to-fine sequence are as follows: similarity
transform optimization of the full model, similarity transform of each
figure (with the structure typicality term measuring figural deviation
from the parent figure), full variation of each medial atom (with the structure
typicality term measuring deviation of the atom from the adjacent atoms).
In a separate program, soon to be combined with the main program, the final
step is boundary offset from the medially implied boundary along its normals.
To date in this program both the structure typicality term and the image
match term measure "distances" from single training case, with no reflection
of variability of the populations. We are applying this method to MRI of
the hand (a test case), CT of the kidney, MRI of the cerebral ventricle,
CT of the pelvic bones, and CT of the spine. By the time of the site visit
in October we anticipate having numerous results with each of these cases
and having begun replacing the distance from the training case metrics
by statistical metrics based on PCA. |
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
Related
Links |
 |
 |
 |
 |
 |
 |
 |
 |
In present dissertation research,
Martin Styner has
begun to develop a method that stabilizes the m-rep description of an object
for shape measurement by determining the medial sampling and figural topology
through statistics from a medial analysis derived from a spherical harmonics
description (Fig. 2).
Paul Yushkevich has begun
the study of coarse-to-fine shape measurement, with the aim of obtaining
descriptions at successive levels of locality and thus high intuitiveness
to users.
Jessica Crouch has begun a dissertation on finite-element based mechanical
modeling of structural change based on coarse-to-fine m-reps models, intended
to achieve two orders of magnitude improvements in speed over previous
3D finite-element methods.
Andrew Thall is well along
in developing methods of computer aided design and rendering of solid objects
via m-reps (Fig. 3).
Robert Katz is largely done
with a dissertation focused on medial representations measuring perceptual
significance of object sections in 2D. This work has some useful implications
for the 3D structural models research, especially the measurement at the
medially implied boundary of related effects of adjacent figures and discrimination
of continuing figures from subfigures via continuity of figural width and
orientation.
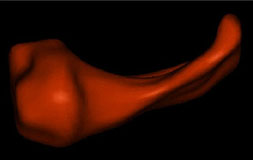 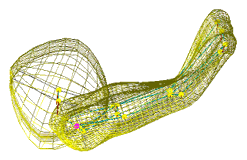 |
| Fig. 2 (Styner).
Left: Hippocampus/amygdala complex (HAC) based on spherical harmonics boundary
representation (SPHARM) from manual segmentation of 3D MRI. Right: Two-figure
m-rep of case at right obtained by deforming m-rep fit to average case.
Average was computed from population of HACs’ SPHARMs. |
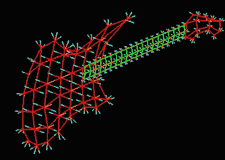 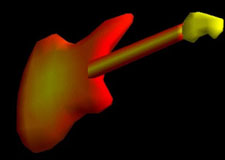 |
| Fig. 3 (Thall) Computer-aided
design of guitar based on m-reps. Left: three meshes of width-proportionally
spaced medial atoms. Right: Rendered guitar. |
|
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
Figural
geometry via statistical analysis of clouds of medial atoms |
 |
 |
 |
 |
 |
 |
 |
 |
In work done here by George Stetten
and illustrated in Fig. 4, images are first analyzed in figural terms without
the aid of a model. Medial atoms are extracted by thresholding from the
image data, and local clouds of the atoms are statistically analyzed to
produce information as to the local existence of a piece of figure and
if it exists, its width, orientation, and geometric type within the space
encompassed by sphere, tube, and slab.
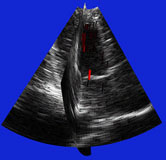 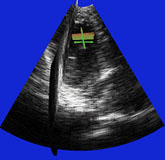 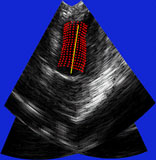 |
| Fig. 4 (Stetten). Right: Automatic
cardiac left ventricle extraction from 3D ultrasound image via axis between
mitral valve and left ventricle. Left: As determined from statistical analysis
of cloud of medial primitives, mitral valve signalling (by red color) its
being a slab and giving its orientation. Middle: Similarly, ventricle body
signaling (by green color) its being a tube and giving its orientation
and size. |
|
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
Cores
and Other Medial Height Ridges |
 |
 |
 |
 |
 |
 |
 |
 |
Both slabs and tubes can be extracted by locating cores, i.e., height
ridges of a graded measure of medial strength that we call "medialness"
(Fig. 5). Height ridges are subdimensional maxima and fall into two categories:
maximal convexity ridges and optimal parameter ridges, which differ according
to the rule used for choosing the subspace in which the medialness maximum
is checked for. Subdimensional saddles connect height ridges when they
stop, forming "connectors". This work involves singularity theoretic study
of height ridges [Damon, Miller, Keller] as well as algorithmic development
of height ridge extractors [Fritsch, Aylward, Furst, Fridman].
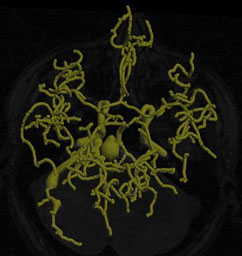 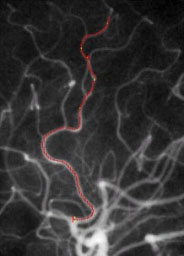 |
| Fig. 5. Left: Tree of blood vessels and aneurysm extracted from magnetic
resonance angiogram via height ridges (Aylward,
Bullitt). Right: Core (red), with connectors (yellow) for a blood vessel
in a (2D) x-ray angiogram (Furst, Fridman). |
|
 |
 |
 |
 |
 |
 |
|