 |
 |
 |
 |
 |
 |
 |
 |
Introduction |
 |
 |
 |
 |
 |
 |
 |
 |
Of the presently available methods for segmentation of anatomic objects
from medical images, principally interactive ones are the most commonly
used in clinical practice. More automatic techniques are based on statistical
pattern recognition (thresholding), mathematical morphology, deformable
models with local geometric constraints (active surfaces), or deformable
structural models, i.e., using models that involve nonlocal spatial relationships.
The methods involving the deformation of structural models seem distinctly
the most successful, and they lend themselves not only to segmentation
but also to shape measurement and registration. It is on these that we
focus. Access to our papers on object segregation and shape representation,
subdivided into topic areas, can be made through the Bibliography
page. A tutorial on object shape representation is available here.
A deformable structural model for one or more objects can be based on
a variety of primitives. Among the possible primitives are voxels (with
intensity) [e.g., Miller, Christensen, Joshi], landmarks [e.g., Bookstein,
Kendall], sampled boundary points [e.g., Cootes & Taylor], parameterized
continuous boundaries [e.g., Kelemen & Gerig, Staib & Duncan],
and medial atoms [Pizer, Siddiqi,
Székely, Kimia]. We focus on medial
methods, especially those based on the m-reps representation (Fig.
1), on the parameterized continuous boundary representation based on spherical
harmonics, and on tubes found by intensity
or medial strength ridges. We are also working to develop methods for the
validation
of our segmentation methods in inexpensive, automatic, generalizable ways.
 |
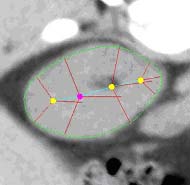 |
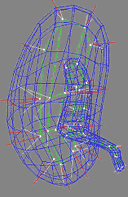
| Fig. 1. An m-rep model for a kidney. Left, in
3D: the m-rep is made from 2 linked figures, each of which is represented
by a mesh or chain of medial atoms. Here the two figures represent the
whole kidney and the pelvis + ureter. The medial atoms are shown in white
with the meshes in green and the medially implied boundaries in blue. Right,
in 2D: a cut through the 3D image data showing 2D medial atoms interpolated
from the 3D atoms for the figure representing the whole kidney. |
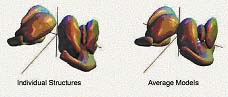
Fig 2. Subcortical brain structures via statistics on spherical harmonics
coefficients. |
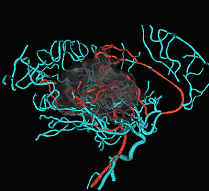
Fig. 3. Tree of vessels extracted from magnetic resonance angiogram,
combined with volume rendered visualization of an arterial-venous malformation. |
|
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
Clinical
Problems |
 |
 |
 |
 |
 |
 |
 |
 |
The deformable models work is driven by a variety of clinical problems:
-
Planning and verification of radiotherapy
-
Neurosciences: science and diagnosis of structures
of the brain and their relation to various mental illnesses
-
Neurosurgery planning and delivery
of neurosurgery involving the vascular system in the brain or involving
the spine
-
Analgesic nephropathy
-
Orthopedic surgery
These problems come both from the UNC
School of Medicine and the Duke
School of Medicine and from collaborating groups at Harvard
University, Johns Hopkins University,
and Memorial Sloan-Kettering Cancer Center.
The problems involve us in segmentation and shape measurement of the cerebral
ventricle from both MRI and 3D ultrasound, segmentation of the pelvic bones
from CT and prostate from MRI, segmentation and shape measurement of the
kidney from CT, segmentation and shape measurement of subcortical brain
structures, especially the hippocampus, from MRI, and successive segmentation
over 26-40 weeks of gestational age of the premature infant's cortex and
basal ganglia from MRI. |
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
Subproject
Links |
 |
 |
 |
 |
 |
 |
 |
 |
The following pages go into further depth in the various aspects of
this project:
|
 |
 |
 |
 |
 |
 |
| |
 |
 |
 |
Participants |
 |
 |
 |
 |
 |
 |
 |
 |
Faculty focusing on methods for segmentation, registration, and shape
measurement include:
-
Stephen Pizer, Kenan Professor
(Computer Science, Radiology, Radiation Oncology, Biomedical Engineering)
-
Guido Gerig, Taylor Grandy
Professor (Computer Science, Psychiatry)
-
Ed Chaney, Professor (Radiation Oncology)
-
Julian Rosenman, Professor (Radiation
Oncology, Computer Science)
-
James Damon, Professor (Mathematics)
-
Stephen Marron, Professor (Statistics)
-
Valen Johnson, Professor (Statistics, Duke)
-
James Coggins, Associate
Professor (Computer Science)
-
Stephen Aylward, Assistant
Professor (Radiology, Computer Science)
|
 |
 |
 |
 |
 |
 |
|