Title: Determining
the Geometry of Boundaries of Objects From medial Data
Author: James Damon
This paper is of particular interest to those in computer science. For those interested in reading further into the mathematical details, see papers I and II below.
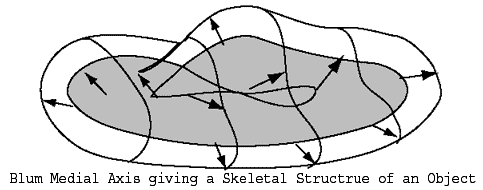
Introduction: For 2D objects in R^2 or 3D objects in R^3 with (smooth) boundaries B, the Blum medial axis M, or an appropriate variant, is a fundamental object for describing shape. There has been a significant body of work devoted to methods for computing it, including the grassfire method, the Hamilton-Jacobi skeleton, and Veronoi methods among others.
Author: James Damon
Introduction: There are a number of constructions which begin with a (piecewise) smooth object and associate to it a singular set which contains information regarding the relative position, geometry and shape for the original object. Examples are the "conflict set" (Maxwell set) associated to a parametrized family of smooth functions, the Voronoi set (skeleton) associated to a collection of regions with (piecewise) smooth boundries, the caustic set for wave front evolution, and the shock set for hyperbolic equations. Several of these methods are used for analyzing shapes in computer imaging and vision, e.g. the Blum medial axis, chordal locus of Brady and Asada, and arc-segment medial axis of Leyton.

Author: James Damon
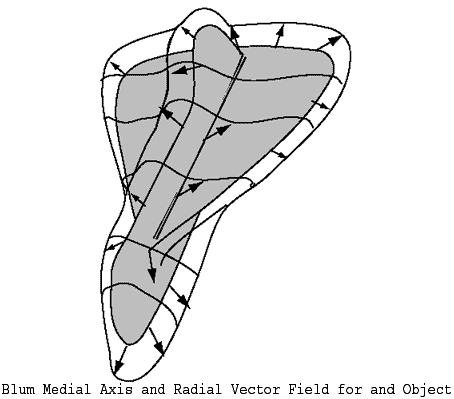
Introduction: In the first part of this paper (paper I above), we introduced the notion of a skeletal structure (M,U) as a generalization of the Blum medial axis M of a region with smooth boundary. It consists of a Whitney stratified set M together with the multivalued radial vector field U from points M to the corresponding points of tagency on the boundary, e.g. Fig. 1.